Resimlerle 'Functor'giller, 'Applicative'giller ve 'Monad'giller
İşte karşınızda basit bir değer: 
ve bu değere bir fonksiyonu (işlevi) nasıl uygulayacağımızı (application) zaten biliyoruz: 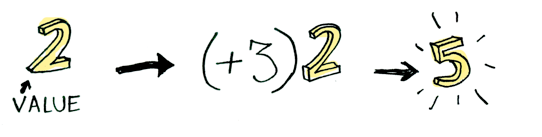
Gayet basit. Şimdi bunu biraz genişletelim: Herhangi bir değer bir bağlam (context) içinde yer alabilir. Şimdilik bağlam deyince aklınıza içinde bir değer saklayabileceğimiz bir kutu gelsin:
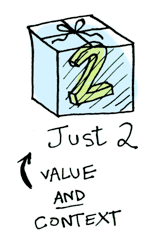
Şimdi bu değere bir fonksiyonu uyguladığınızda bağlama göre değişen farklı sonuçlar elde edersiniz. İşte bu, bütün 'Functor'giller, 'Applicative'giller ve 'Monad'gillerin altında yatan fikirdir. Maybe veri tipi birbiriyle ilişkili iki bağlam tanımlar:
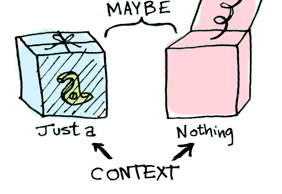
data Maybe a = Nothing | Just a
Az sonra elimizdeki şeyin Just a ya da bir Nothing olduğuna bağlı olarak fonksiyon uygulamasının nasıl farklılaştığını göreceğiz. Şimdi, Öncelikle 'Functor'gillerden konuşalım!
'Functor'giller
Değer bir bağlamın parçası olduğunda, normal bir fonksiyonu o değer üzerinde uygulamamız mümkün değildir:

Bu noktada fmap devreye girer. fmap sokakların çocuğu, bağlamlarla iş yapmaya alışkın. fmap bir bağlamın parçası olan değerlere fonksiyonların nasıl uygulanacağını bilir. Örneğin, diyelimki (+3)'ü Just 2'ye uygulamak istiyorsunuz. fmap'i kullanmalısınız:
> fmap (+3) (Just 2)
Just 5
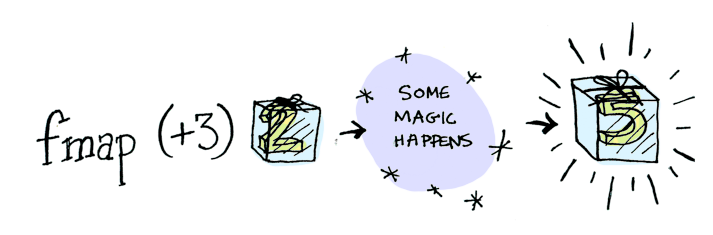
Ta-taaa!
fmap bize nasıl yapılacağını gösterir. Peki fmap fonksiyonu nasıl uygulacağını nasıl biliyor?
De bana, sahi nedir Functor?
Functor halis muhlis bir typeclass'dır. İşte bu da tanımı:

Bir Functor aslında kendi üzerinde fmap'in nasıl uygulanacağını tanımlayan herhangi bir veri tipinden başka bir şey değil. Bakın fmap işte böyle çalışır:
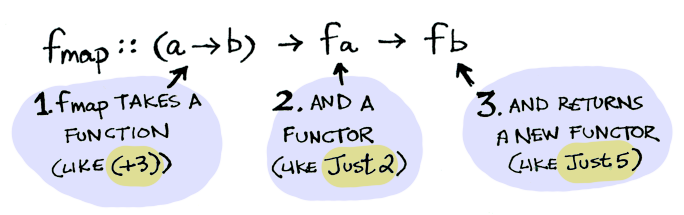
O yüzden de şunu yapabiliriz:
> fmap (+3) (Just 2)
Just 5
Ve fmap sihirli bir şekilde bu fonksiyonu uygular. Çünkü Maybe de sonuçta bir Functor'dır ve fmap'in Justlara ve Nothinglere nasıl uygulanacağını açıkça belirtmiştir:
instance Functor Maybe where
fmap func (Just val) = Just (func val)
fmap func Nothing = Nothing
fmap (+3) (Just 2) yazdığımızda arkada şunlar olur:
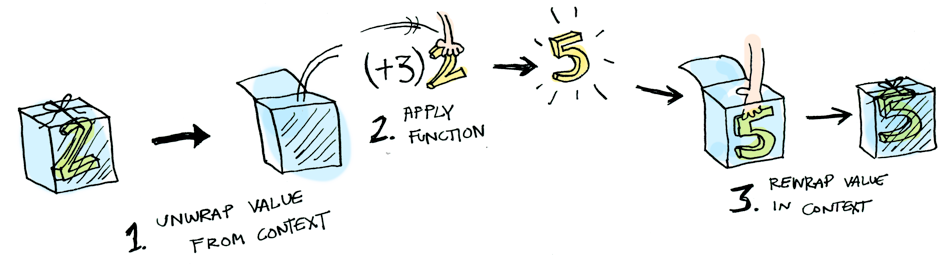
Belki de sabırsızsınız ve "hadi fmap, lütfen (+3)ü Nothinge uygula" demek istiyorsunuz?

> fmap (+3) Nothing
Nothing

Bill O’Reilly, Maybe functor'ından tamamen habersizce...
Matrix'deki Morpheus gibi, fmap sadece ne yapması gerektiğini bilir; Nothingle başlar, Nothingle bitirirsiniz! fmap 'zen'dir. Şimdi Maybe veri tipinin varlığı anlam kazanmaya başlıyor. Mesela, Maybeden yoksun bir dilde veri tabanı kayıtlarıyla böyle çalışırsınız:
post = Post.find_by_id(1)
if post
return post.title
else
return nil
end
Bir de Haskell'e bakın:
fmap (getPostTitle) (findPost 1)
Eğer findPost geçerli bir post dönerse, getPostTitleile post'un title'ını elde ederiz. Yok eğer Nothing dönerse, biz de Nothing döneriz! Nasıl? Çok havalı di mi! <$> ise fmapin daha sık rastlayacağınız infix versiyonu:
getPostTitle <$> (findPost 1)
Başka bir örnek daha: Bilin bakalım bir fonksiyonu bir listeye uyguladığımızda ne olur?
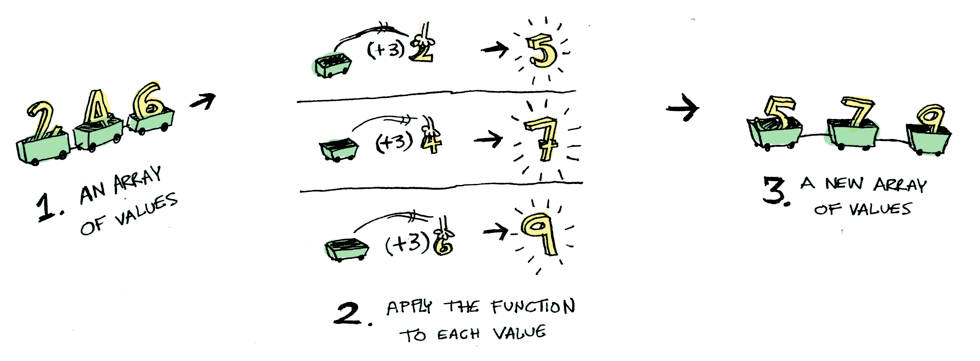
List veri tipi de bir functor'dır! Bakalım nasıl tanımlanmış:
instance Functor [] where
fmap = map
Peki, peki, son bir örnek: Bir fonksiyonu diğer bir fonksiyona uyguladığınızda ne olur?
fmap (+3) (+1)
İşte size bir fonksiyon:
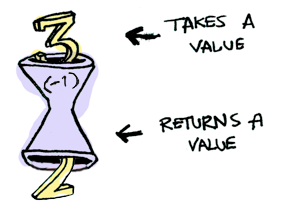
Bu da bir fonksiyon üzerinde giğer bir fonksiyonun uygulaması:
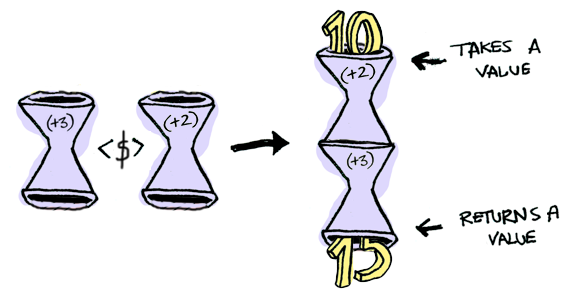
Sonuç mu? Yeni, başka bir fonksiyon!
> import Control.Applicative
> let foo = fmap (+3) (+2)
> foo 10
15
Bu da demek oluyor ki fonksiyonlar da 'Functor'gillerdendir!
instance Functor ((->) r) where
fmap f g = f . g
Bir fonksiyon üzerinde fmap uyguladığınızda, aslında yaptığınız şey fonksiyon bileştirmeden (function composition) başka bir şey değil!
'Applicative'giller
'Applicative'giller işi bir üst seviyeye taşır. Applicative kullandığımızda da değerlerimiz bir bağlamın parçasıdırlar, aynen 'Functor'gillerdeki gibi:

Farklı olan ise bu kez fonksiyonlarımızın da bir bağlamın parçası olması!

Öncelikle, bunu bi içinize sindirin. 'Applicative'giller şaka sevmez. Control.Applicative içinde tanımlanan <*> bir bağlamın içine yerleştrilmiş bir fonksiyonun gene bir bağlamın parçası olan bir değere nasıl uygulanacağını bilir:
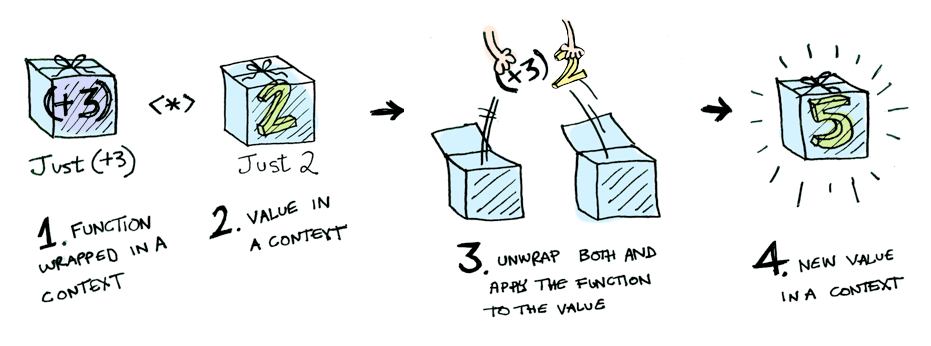
Misal:
Just (+3) <*> Just 2 == Just 5
<*>ın kullanımı bazı beklenmedik, ilginç durumları ortaya çıkarabilir. Örneğin:
> [(*2), (+3)] <*> [1, 2, 3]
[2, 4, 6, 4, 5, 6]
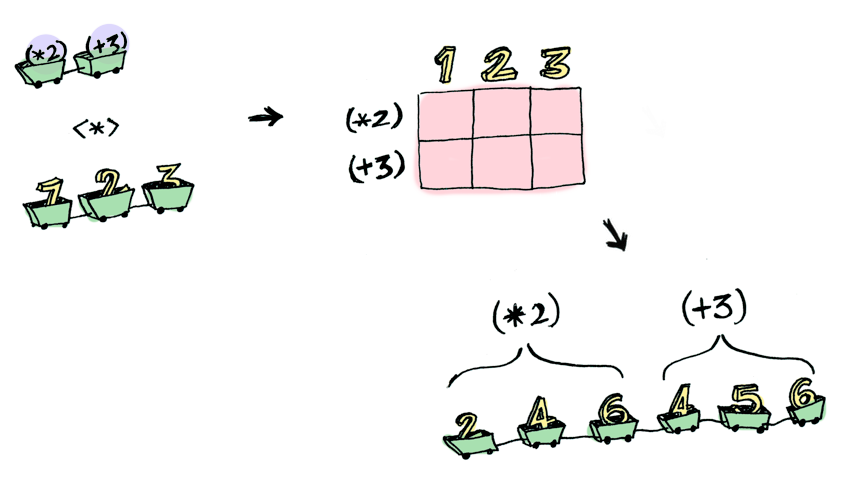
Gelin 'Functor'gillerle yapamayacağınız ama 'Applicative'gillerle mümkün olan bir şeye bakalım. İki argümanlı bir fonksiyonu (bir bağlam içinde) paketlenmiş iki değere nasıl uygularsınız?
> (+) <$> (Just 5)
Just (+5)
> Just (+5) <$> (Just 4)
ERROR ??? WHAT DOES THIS EVEN MEAN WHY IS THE FUNCTION WRAPPED IN A JUST
'Applicative'giller:
> (+) <$> (Just 5)
Just (+5)
> Just (+5) <*> (Just 3)
Just 8
Applicative Functorı yerinden eder. “Yetişkinler, kaç argümanı olduğunun önemi yok, istediği fonksiyonu kullanabilir” der. “Cephanemde <$> ve <*> varken, kaç argümanlı olduğuna bakmadan herhangi bir fonksiyonu kullanabilir, sonra da ona paketlenmiş bütün değerleri geçirir ve karşılığında da paketlenmiş değeri alırım! AHAHAHAHAH!”
> (*) <$> Just 5 <*> Just 3
Just 15
Bir dakika! Aynı şeyi yapan liftA2 adında bir fonksiyon var zaten:
> liftA2 (*) (Just 5) (Just 3)
Just 15
'Monad'giller
'Monad'gilleri öğrenmenin bir kaç yolu var:
- Bilgisayar Bilimlerinde Doktora yap.
- Unut gitsin! Çünkü bu bölüm için ona ihtiyacın yok!
'Monad'giller yeni bir fırsat sunar.
'Functor'giller paketlenmiş bir değere bir fonksiyonu uygularlar:
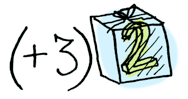
'Applicative'giller paketlenmiş bir fonksiyonu paketlenmiş bir değere uygularlar:
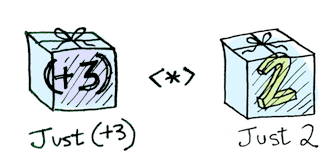
'Monad'giller paketlenmiş bir değer dönen bir fonksiyonu paketlenmiş bi değere uygularlar. 'Monad'giller bunu sahip oldukları >>= (İngilizce “bind” olarak söylenir) fonksiyonu ile yaparlar.
İyisi mi bir örnek üzerinden gidelim. Eski dostumuz Maybe de bir monad:

Kendi halinde takılan bir monad: Just a
Farz edelim ki half sadece çift sayılarla çalışan şahsına münhasır bir fonksiyon:
half x = if even x
then Just (x `div` 2)
else Nothing
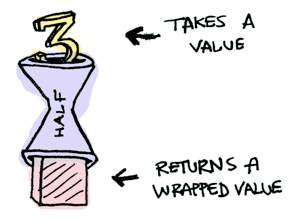
Muhtereme paketlenmiş bir değer geçmeye çalışırsak ne olur?

Paketlenmiş değeri kendisine itelemek için kullanmamız gereken şey >>=. Halk arasında >>=:

Bir de nasıl çalıştığına bakalım:
> Just 3 >>= half
Nothing
> Just 4 >>= half
Just 2
> Nothing >>= half
Nothing
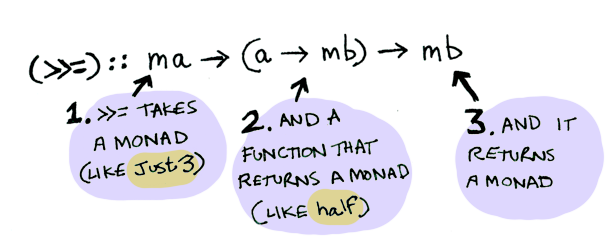
Sahi arka planda neler dönüyor? Monad da başka bir typeclass ve şu da kısmi tanımı:
class Monad m where
(>>=) :: m a -> (a -> m b) -> m b
Biraz daha açarsak, >>= şöyle bir şey:
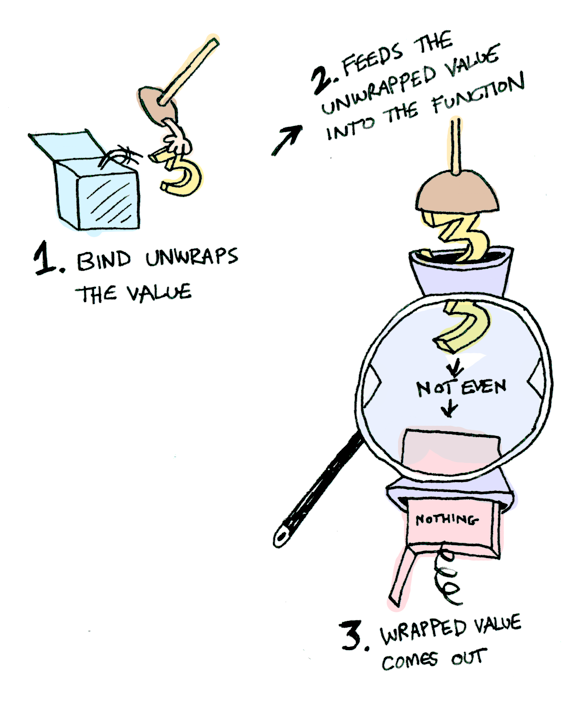
Maybe de bir Monad:
instance Monad Maybe where
Nothing >>= func = Nothing
Just val >>= func = func val
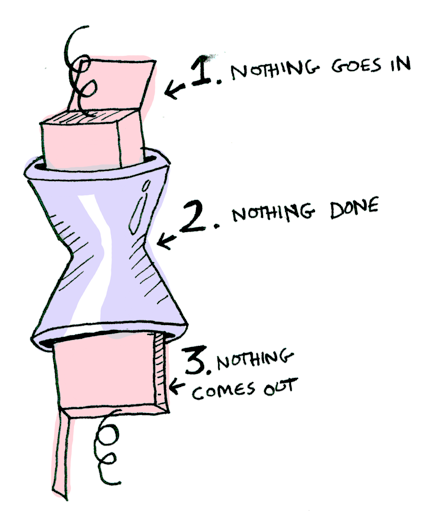
Burada kendisini Just 3 kılığında iş üstünde görüyoruz!
Nothing geçtiğinizde işler daha da basitleşir:
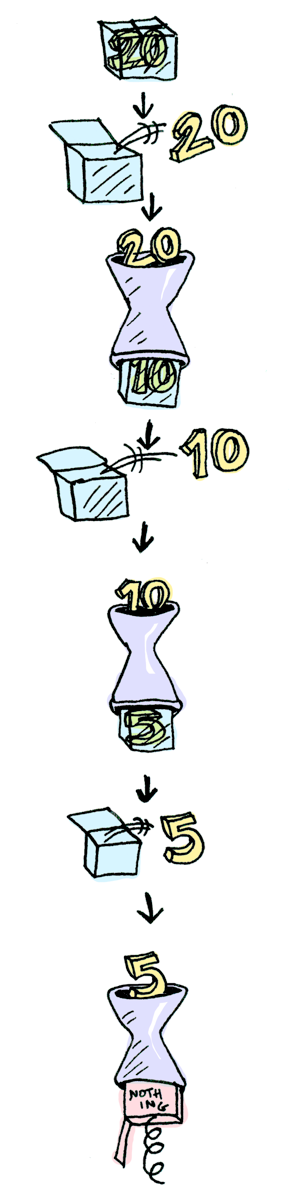
Şu şekilde zincirleme çağrılar da yapabilirsiniz:
> Just 20 >>= half >>= half >>= half
Nothing

Çok havalı! An itibariyle Maybenin bir Functor, bir Applicative, ve bir Monad olduğunu biliyoruz.
Şimdi de başka bir örnek üzerinden gidelim: IO monadı:
Belli üç fonksiyonumuz var. getLine argümanı yok, kullanıcıdan girdi alır:

getLine :: IO String
readFile bir dosya ismi (string) alır ve karşılığında o dosyanın içeriğini döner:

readFile :: FilePath -> IO String
putStrLn bir string alır ve onu yazdırır:

putStrLn :: String -> IO ()
Fonksiyoların üçü de sıradan bir değer (ya da hiçbirşey) kabul eder ve karşılığında paketlenmiş bir değer döner. Biz de bu fonksiyonları >>= yardımıyla zincirleyerek kullanabiliriz.!
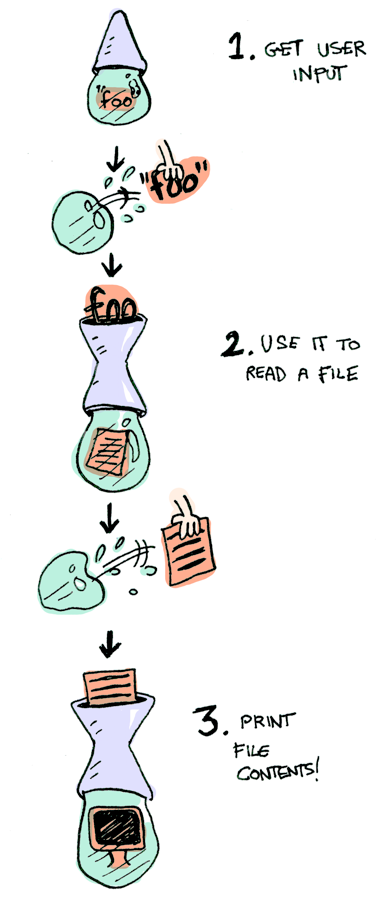
getLine >>= readFile >>= putStrLn
İşte bu! Monad gösterisine ön sıradan koltuklar var! İzlemeyen kalmasın!
Haskell, monadların kullanımı için bazı güzellikler (syntactical sugar) sunar ki biz buna do notasyonu diyoruz:
foo = do
filename <- getLine
contents <- readFile filename
putStrLn contents
Sonuç
- Bir functor
Functortypeclass'ının gereklerini yerine getiren bir veri tipidir. - Bir applicative
Applicativetypeclass'ının gereklerini yerine getiren bir veri tipidir. - Bir monad
Monadtypeclass'ının gereklerini yerine getiren bir veri tipidir. Maybeüçününde gereklerini yerine getirdiği için hem bir functor, hem bir applicative hem de bir monad'dır.
Üçü arasındaki fark nedir?

-
functorgiller: paketlenmiş bir değere
fmapveya<$>kullanarak bir fonksiyonu uygularsınız -
applicativegiller: paketlenmiş bir değere gene paketlenmiş bir fonksiyonu
<*>veyaliftAyoluyla uygularsınız -
monadgiller: paketlenmiş bir değer dönen bir fonksiyonu paketlenmiş bir değere
>>=veyaliftMyoluyla uygularsınız
Sözün özü, değerli arkadaşım (bu noktadan sonra artık arkadaş olduğumuzu düşünüyorum), sanırım ikimiz de monadgillerin kolay ve zekice bir fikir olduğunda hemfikiriz. Bu rehberle tadını aldıktan sonra 'İdare edemem Anne!' diyorsan eğer LYAH’in Monadgiller kısmına gözatabilirsin. Atladığım çok şey var çünkü zaten Miran bu konuda etraflıca bilgi verirken mükemmel bir iş çıkarmış.
Çeviri
Çeviri Cem Eliguzel tarafından "Bu sefer her şey aydınlanacak!" hezeyanlarından birinde bir bayram sabahı kaleme alınmıştır.
Orijinal metin Aditya Bhargava tarafından kaleme almıştır.
Çeviriye katkıda bulunmak için bana bir e-mail atabilir ya da bir github pull request gönderebilirsiniz.